|
(このページは該当講座受講登録者向けの情報です)
◆全員ブラインドタッチが出来るようにすること。
練習用ソフトは何でも良いのですが、例えば下記を使ってとにかく 1日15分 を連続15日間続けて下さい。
チェックテスト 寿司打(サウンドなしでやりましょう)
http://typing.sakura.ne.jp/sushida/index.html
速度はこの寿司打で、平均キータイプ数が 2.3回/秒 を超えないとダメです。
HTML入門
演習:自分の学生番号と名前を表示する
演習用HTML(右クリックして保存)
課題:自分で写真を撮って自己紹介ページを作る
課題用サンプルHTML(右クリックして保存)
課題用画像サンプル(右クリックして保存)
HTMLファイルで画像が表示されない場合は、セキュリティーのためにブロックが掛っている場合がある。その際にはHTMLファイルを右クリック-[プロパティ]→下の方の[ブロックの解除]を選択する。
表を使ったHTML:1Qと2Qの各自の時間割を1つのWebページに上下で表示する
テーブルの課題サンプル(右クリックして保存)
ハイパーテキストの課題サンプル(右クリックして保存)
JavaScriptを使ったWebプログラミング
Web プログラミング入門
Web プログラミング入門(演習用サンプルファイル)
エクセルを使った回帰分析
サンプルデータ
---------------------------------------
プログラムを基礎から勉強する場合:Python入門の無料E-Learning環境(paizaラーニング)_ブラウザ画面上で実行できます)
Pythonによるプログラミング入門
Python実行環境 Google Colaboratory (下記URLで、すぐにクラウド上でPythonが使えるようになります)
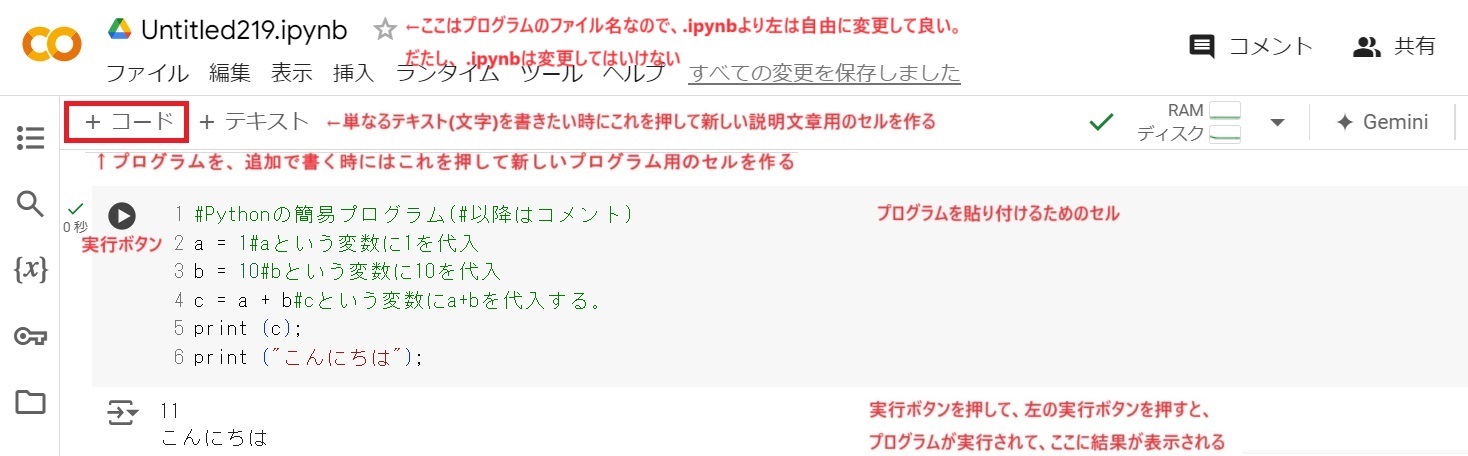
「ノートブックを新規作成」を押して新しくページを作ってから、四角いセルにプログラムを入力して、左の丸と三角のボタンを押すと実行できます。
Google Colaboratory Python実行環境
---------------------------------------
PythonによるAIプログラミング入門 サンプルプログラム集
Google Colaboratoryに下記ソースプログラムを貼り付けて実行して下さい。
------から------までの区間が1つのプログラムです。例えば次の#Pythonの簡易プログラム・・・からprint ("こんにちは");までの6行をコピーしてColaboratoryに貼り付けて実行して下さい。)
---------------------------------------
#Pythonの簡易プログラム(#以降はコメント)
a = 1#aという変数に1を代入
b = 10#bという変数に10を代入
c = a + b#cという変数にa+bを代入する。
print (c);
print ("こんにちは");
---------------------------------------

---------------------------------------
#Pythonの簡易プログラム(#上記と全く同じ処理で、;を使うと1行に複数の命令を書くことが出来る)
a = 1; b = 10; c = a + b
print (c);
print ("こんにちは");
---------------------------------------
#aという変数に1を代入し、bという変数に10を代入して、cという変数にa+bを代入する。
#繰り返し命令の例
list=[0,1,2]
for i in list:
print(i)#←字下げをしている部分が、繰り返しの範囲
#結果← これより下の結果はプログラムを実行した結果となるので、Google Colaboratoryに入力不要です。以下全て同様です。
#0← 結果の箇所の一番左の#は、この行を間違えてGoogle Colaboratoryに入力しても動くようにコメント#にしています。
#1
#2
---------------------------------------
#繰り返し命令の例 字下げで繰り返しの範囲を指定する 同じ処理ですが、繰り返しが100回とか、増えても記載が短くて済む
for i in range(3):#0から始まって1,2まで実行する。Rangeで指定した回数だけ実行する
print(i)
#結果
#0
#1
#2
---------------------------------------
#結果に説明の文字を加える時は、整数のiも文字型strにする(この+記号は足し算では無く、文字列の連結の意味になる)
for i in range(3):
print("i = " + str(i))
#結果
#i = 0
#i = 1
#i = 2
---------------------------------------
#条件分岐の例 条件分岐も 字下げで条件の範囲を指定する
even=0#偶数の合計
odd=0#奇数の合計
sum=0#合計
for i in range(10):#変数i=0.1,2,3,4,5,6,7,8,9 と代入して、10回実行する。
if i%2==0:#2で割った余りが0なら偶数
even=even+1
sum = sum+1
else:#2で割った余りが0でないなら奇数
odd = odd+1
sum = sum+1
print("合計 = " + str(sum))
print("偶数の合計 = " + str(even))
print("奇数の合計 = " + str(odd))
---------------------------------------
#多重繰り返し処理とデータフレーム
import copy # 列情報をコピーして代入する処理があるためにライブラリを読み込む
import pandas as pd # データフレームを利用するためpandasライブラリを読み込む
columns = [] # 列情報を格納するためのリスト変数
indexs = [] # 行列情報を格納するためのリスト変数
for column in range(1, 10): # 列columnの繰り返しループ:1の段から9の段まで(10の前まで実行)
for line in range(1, 10): # 行lineの繰り返しループ:1の段から9の段まで(10の前まで実行)
columns.append(column * line) # 九九を計算した積の結果を列リスト変数に順次追加する
indexs.append(copy.copy(columns)) # 行列リスト変数indexsに、列情報(列リスト変数columns)に追加する
columns.clear() #新しい計算をするために、古いデータが入っている列リスト変数columnsを初期化する
print("indexsの表示")
print(indexs) # 画面にindexsという行列リストを表示するが見にくい
df = pd.DataFrame(indexs) # 九九一覧がindexsという行列リストに入っているので、見やすくするためデータフレームに変換する
print("indexをデータフレームで表示")
df.head(9) # 画面にindexsという行列リストを表示するが改行されないので見にくい
# 実行結果 indexsの表示としてindexsという行列リストを表示しているが1つの行になってしまい、見にくいので、データフレームdfを使って方が見やすくしている。

---------------------------------------
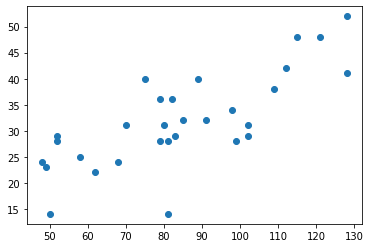
#散布図を表示するプログラム
import matplotlib.pyplot as plt # 散布図を描画するためにグラフ描画ライブラリを読み込む
#x座標 来客数 1日目の来客数,2日目の来客数,・・・
visitors =[62,70,81,68,82,58,50,79,83,102,81,109,48,52,75,99,102,115,98,52,49,85,79,91,121,128,80,89,112,128]
#y座標 その(xの)来客数の日に、ドリンクが売れた数
energyDrink =[22,31,28,24,36,25,14,28,29,31,14,38,24,28,40,28,29,48,34,29,23,32,36,32,48,41,31,40,42,52]
plt.plot(visitors, energyDrink, 'o') #plot(x座標,y座標,種類)で結果の散布図をプロットする。o:丸 等
plt.show() # 散布図を画面に表示させる
---------------------------------------
#散布図に回帰直線を表示するプログラム
from sklearn.linear_model import LinearRegression#線形回帰分析用ライブラリ
import matplotlib.pyplot as plt #図形を描画する図形描画ライブラリ
import pandas as pd#データ分析ライブラリ
import math#乱数や数学関数を利用するためのライブラリ
import seaborn#図形を綺麗に描画するためのツール
visitors =[62,70,81,68,82,58,50,79,83,102,81,109,48,52,75,99,102,115,98,52,49,85,79,91,121,128,80,89,112,128]#1日の来店人数
energyDrink =[22,31,28,24,36,25,14,28,29,31,14,38,24,28,40,28,29,48,34,29,23,32,36,32,48,41,31,40,42,52]#1日のエナジードリンクの売上本数
beers =[31,30,46,34,35,30,28,40,34,58,39,53,20,28,31,51,56,60,44,22,29,43,35,47,57,69,40,42,67,64]# 1日のビールの売り上げ本数
modelLR = LinearRegression()#線形回帰にLinearRegressionクラスの利用を指定する
modelLR.fit(pd.DataFrame(visitors), pd.DataFrame(energyDrink))#fit(x座標,y座標)データを基に線形回帰分析を実行
plt.plot(visitors, energyDrink, 'o')#plot(x座標,y座標,種類)で結果の散布図をプロットする。o:丸、s:四角形、D:菱形 等
plt.plot(visitors, modelLR.predict(pd.DataFrame(visitors)), linestyle="solid")#図中に回帰直線を描画する
plt.show()
print('モデル関数の回帰変数 w1: %.3f' %modelLR.coef_)
print('モデル関数の切片 w2: %.3f' %modelLR.intercept_)
print('y= %.3fx + %.3f' % (modelLR.coef_ , modelLR.intercept_))
R2= modelLR.score(pd.DataFrame(visitors), pd.DataFrame(energyDrink))#決定係数R^2の算出
print('決定係数 R^2: ', R2)
print('(決定係数 R^2=回帰係数 r^2より)回帰係数 r = ',math.sqrt(R2))
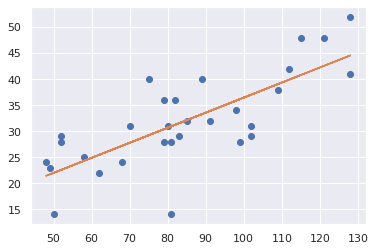
#課題 これを基に30代の人数と、缶ビールの売り上げ本数の回帰分析をしなさい
---------------------------------------
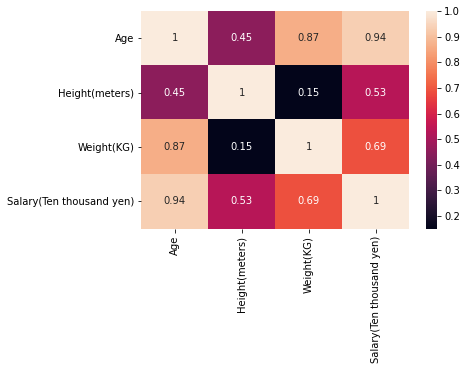
#相関係数行列の計算
import numpy as np #行列計算ライブラリ
import pandas as pd # データを表形式で処理が可能なpandasを読み込む
import matplotlib.pyplot as plt #図形を描画する図形描画ライブラリ
import seaborn as sns#seabornでグラフを見栄え良くするライブラリ
#%matplotlib inline#プログラムの情報出力を黒い画面では無く、JupitarNotebookに表示させる(GoogleColaboratoryでは使えないので#でコメントアウトで無効にする必要がある)
#ファイルの読み込み
df = pd.DataFrame({
'Name': ["Tanaka", "Aoyama", "Mizuno", "Suzuki", "Uchida", "Watanabe"],
'Age': [25, 45, 52, 22, 23, 41],
'Height(meters)': [1.65, 1.75, 1.75, 1.65, 1.75, 1.65],
'Weight(KG)': [69, 75, 75, 60, 63, 78],
'Salary(Ten thousand yen)': [450, 780, 1200, 400, 420, 650]
})
corrmat = df.corr()#相関係数行列を求める
f, ax = plt.subplots(figsize=(6, 4))#subplotsはfとaxを返す。figsize=(6, 4)は横が6で縦が4の描画サイズ。f Figure:グラフを描画するキャンバス全体のオブジェクト ax Axes:Figureオブジェクト内の個々のグラフのオブジェクト
sns.heatmap(corrmat, annot=True);#seabornで相関係数行列corrmatを濃淡で可視化する。annot=Trueでセル中に数値を表示する。
---------------------------------------
#CSV(Comma Separated Values)ファイルからデータをデータフレームに読み込む方法
# エクセルなどでcsv形式(文字コードUTF-8)で保存する。文字コードが指定出来なければcsvに保存した後でメモ帳で開いてUTF-8で上書保存する。
calendar2022_9.csv
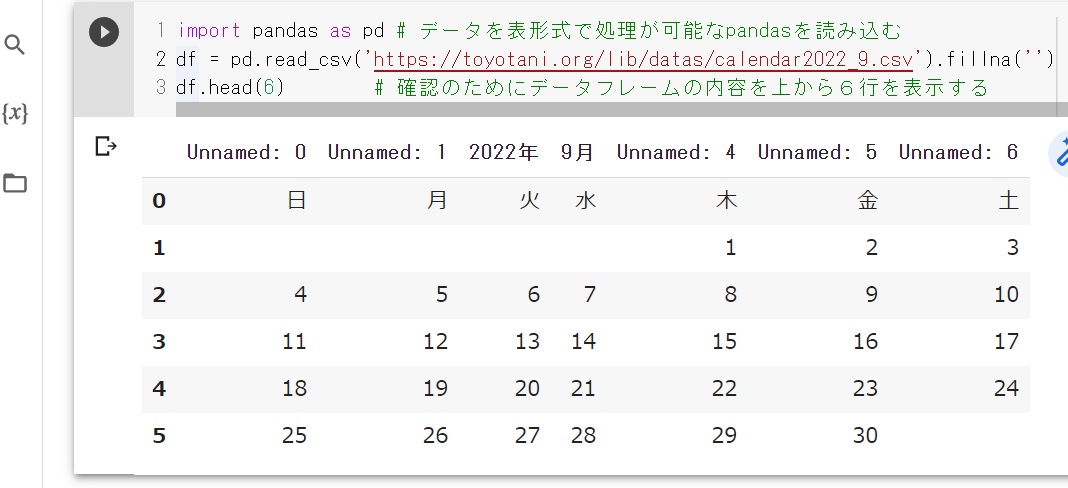
import pandas as pd # データを表形式で処理が可能なpandasを読み込む
df = pd.read_csv('https://toyotani.org/lib/datas/calendar2022_9.csv').fillna('') # 外部のcsvデータ(メモ帳などで文字コードをUTF-8にしておく)を、numpyのdf(データフレーム)に読み込む。データの無い箇所はNan(Not a Number)が自動代入されるので、Nanは見栄えが悪いのでfillna('')ですべて空文字に置き換える
#df = pd.read_csv('calendar2022_9.csv').fillna('') # 自分のデータをアップしたらこちらにする。データの無い箇所はNan(Not a Number)が自動代入されるので、Nanをfillna('')ですべて空文字に置き換える
df.head(6) # 確認のためにデータフレームの内容を上から6行を表示する
# 実行結果 csvの1行目が本来はデータの各項目を入力すべきだが、年と月のデータを入れているために下記のように列名の中に年と月が表示されている
# これが嫌な場合は csvの1行目に ,,,,,,と追加して、2行目からデータを記載すると良い。下記の1行目の,,,,,,は7列分の空データをカンマ6つで区切って入力している。そうする事で1行目は列の項目名であり、空項目が代入され、年と月の行は2行目以降のデータ行として表示される。
 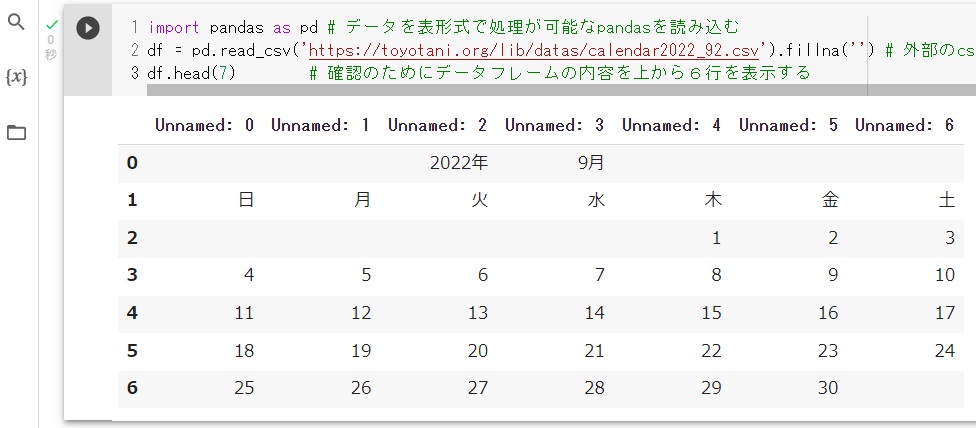
---------------------------------------
#エクセルファイルからデータをデータフレーム(2次元の表を扱うオブジェクト(ツール))に読み込む方法
# 元のエクセルデータ
calendar2022_9.xlsx
import pandas as pd # データを表形式で処理するデータフレームを利用するためにpandasを読み込む
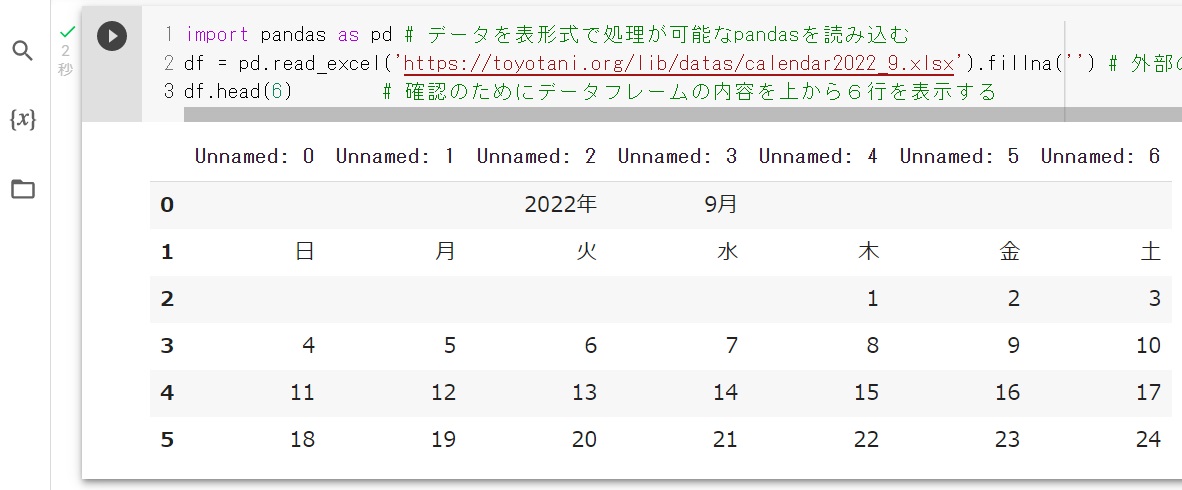
df = pd.read_excel('https://toyotani.org/lib/datas/calendar2022_9.xlsx').fillna('') # 外部のエクセルデータを、データフレームの変数dfに読み込む。データの無い箇所はNan(Not a Number)が自動代入されるので、Nanをfillna('')ですべて空文字に置き換える
df.head(6) # 確認のためにデータフレームの内容を上から6行を表示する
# 実行結果
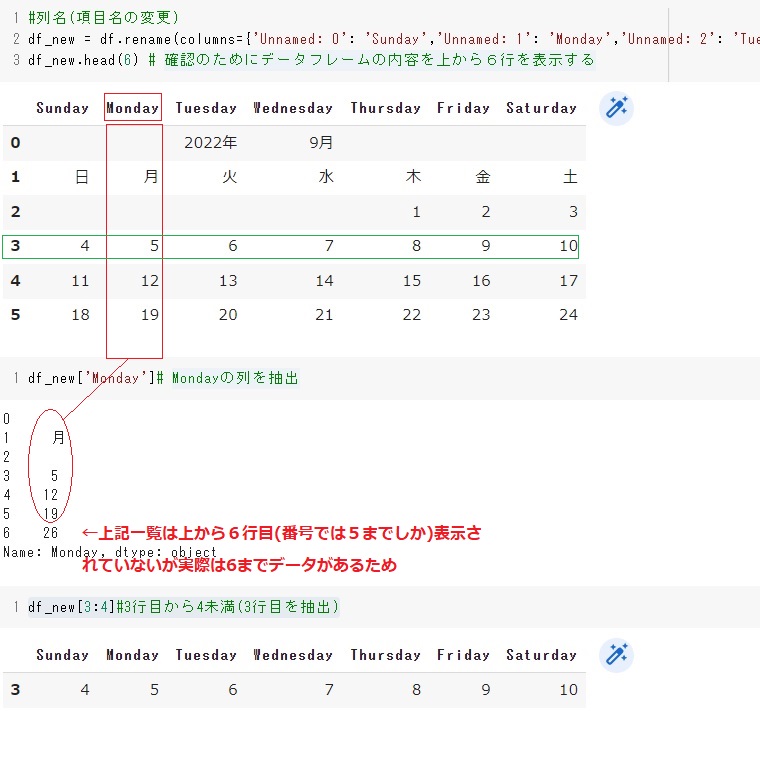
#列名(項目名の変更:新たにdf_newというデータフレームを作成して、そこに新しい項目名にする)
df_new = df.rename(columns={'Unnamed: 0': 'Sunday','Unnamed: 1': 'Monday','Unnamed: 2': 'Tuesday','Unnamed: 3': 'Wednesday','Unnamed: 4': 'Thursday','Unnamed: 5': 'Friday','Unnamed: 6': 'Saturday',})
df_new.head(6) # 確認のためにデータフレームの内容を上から6行を表示する
df_new['Monday']# Mondayの列を抽出
df_new[3:4]#3行目から4未満(3行目を抽出)
---------------------------------------
#CSV(Comma Separated Values)ファイルからデータを読み込んで相関係数行列を求める方法
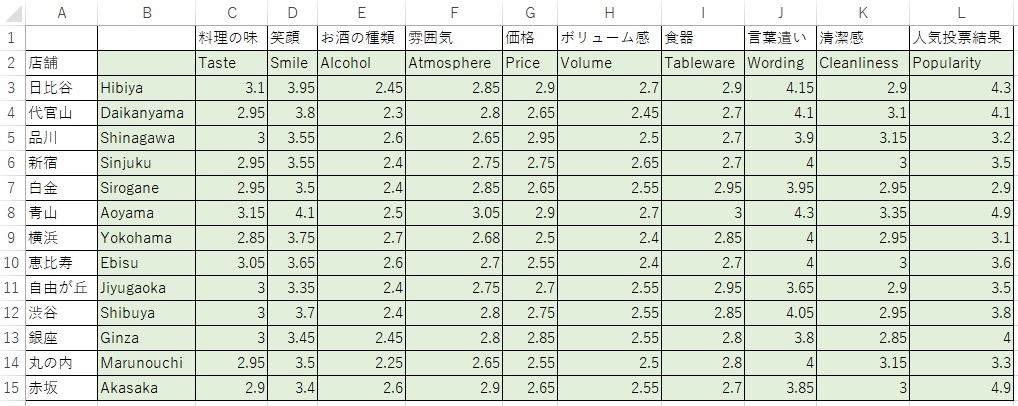
#上記のようなエクセルファイルを、カンマで区切られたCSV形式のファイルに変換する。エクセルでcsv形式(文字コードUTF-8)で保存する。文字コードが指定出来なければcsvに保存した後でメモ帳で開いてUTF-8で上書保存する。
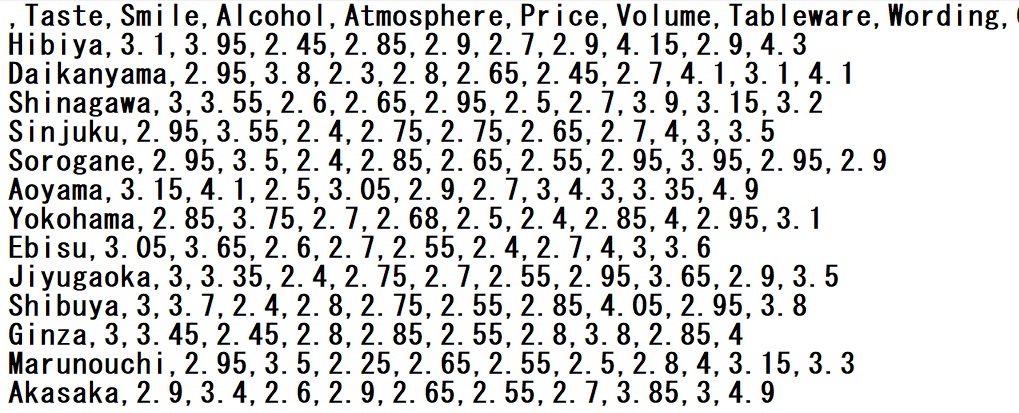
#右をクリックするとダウンロードできるので、それを動画を参考にGoogleColaboratoryにアップするCorrelation.csv
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('Correlation.csv')
corrmat = df.corr()#相関係数行列を求める
f, ax = plt.subplots(figsize=(6, 4))#subplotsはfとaxを返す。figsize=(6, 4)は横が6で縦が4の描画サイズ。f Figure:グラフを描画するキャンバス全体のオブジェクト ax Axes:Figureオブジェクト内の個々のグラフのオブジェクト
sns.heatmap(corrmat, annot=True);#seabornで相関係数行列corrmatを濃淡で可視化する。annot=Trueでセル中に数値を表示する。
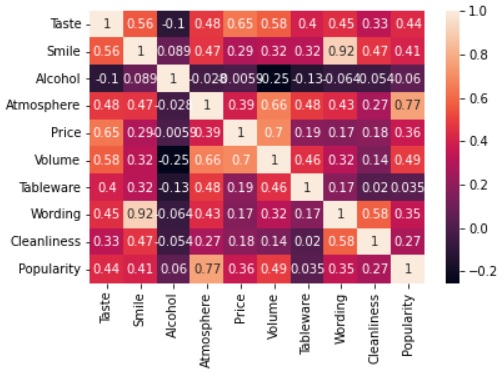
---------------------------------------
#K-meansによるクラスタリング分析:教師なし学習
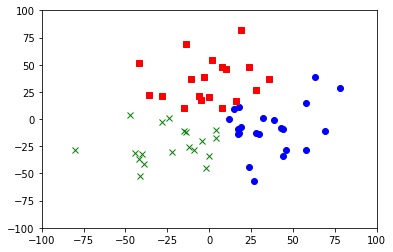
#アンケートを行った結果 横軸に炭酸の強さ、縦軸に甘さをプロットすると次のようになった
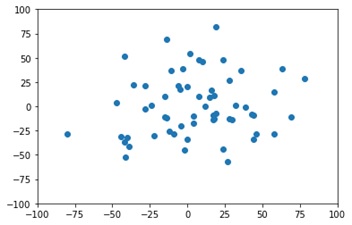
#「炭酸の強さ」と「甘み」を-100から100までの間で好きな値を回答し、横軸に炭酸、縦軸に甘みとしてプロットする。
import numpy as np
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt
#炭酸の強さの好み -100 to 100
coca_x = np.array([-41, -9, 19, 10, -80, -28, 18, -3, -15, -42, -5, -36, -39, -24, -4, -47, 0, 2, -12, -14, -22, 18, 0, -15, 4, -40, -6, -44, -28, -42, 17, 39, 69, 32, 30, -2, 28, 24, 44, 16, 8, 78, 19, 58, -11, 15, 27, 58, -14, 28, 36, 24, 12, 8, 4, 44, 43, 63, 17, 46])
#甘さの強さ -100 to 100
coca_y = np.array([-52, -28, -7, 46, -28, -3, -13, 39, -11, 52, 18, 22, -41, 1, -20, 4, 20, 54, -26, 69, -30, 11, -34, 10, -17, -32, 21, -31, 21, -37, -9, -1, -11, 1, -14, -45, 27, 48, -9, 17, 48, 29, 82, -28, 37, 9, -57, 15, -12, -13, 37, -44, 0, 10, -10, -34, -8, 39, -14, -28])
# 1次元目をcoca_x(炭酸),2次元目をcoca_y(甘さ)とする行列を作成
coca = np.c_[coca_x, coca_y]
#x軸とy軸の幅を設定する
plt.xlim([-100, 100]) #X軸が-100から100まで
plt.ylim([-100, 100]) #Y軸が-100から100まで
#散布図を作成
plt.scatter(coca_x, coca_y)#x,yの散布図をプロットする
plt.show()
kmeans = KMeans(n_clusters=2)
kmeans_model = kmeans.fit(coca)
print(kmeans_model.labels_)

# 色とマーカーの形を設定
colors = ['b','r','g']#b:Blue、r:Red、g:Green
markers = ['o','s','x']#o:〇印、s:□、x:×
for i, l in enumerate(kmeans_model.labels_):# kmeans_model.labels_の中にグループ0と1で分類される。iは各点のデータの数(全データ)をループする。lはクラスタの分類数(2や3)だけループする。
plt.plot(coca_x[i],coca_y[i], color=colors[l],marker=markers[l], ls='None') #0は青の丸、1は赤の四角
plt.xlim([-100, 100])
plt.ylim([-100, 100])
plt.show()
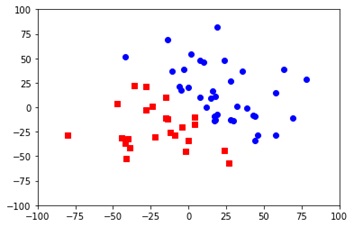
---------------------------------------
#決定木による機械学習:教師あり学習
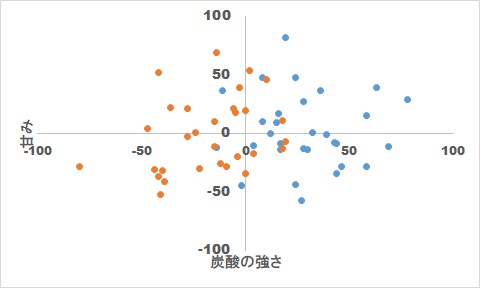
#アンケートを行った結果、Cコーラが好きな人(青)、Pコーラが好きな人(オレンジ)をプロットすると次のようになった。
#決定木を表示させるには、まず次を実行して決定木を表示させるツールを組み込む必要がある
!sudo apt install graphviz
!pip install dtreeviz
---------------------------------------
#次をセルに貼り付けて実行して決定木を表示させる
import numpy as np
from sklearn import tree
from sklearn.tree import plot_tree
from sklearn.tree import export_graphviz
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # 元データを学習用と評価用に自動分割するプログラムを読み込む処理
from sklearn.metrics import accuracy_score # 推測結果を評価をする際に便利なライブラリ(プログラム群)
from six import StringIO
import pydotplus
from IPython.display import Image
#炭酸の強さの好み -100 to 100
coca_x = np.array([ -41, -9, 19, 10, -80, -28, 18, -3, -15, -42, -5, -36, -39, -24, -4, -47, 0, 2, -12, -14, -22, 18, 0, -15, 4, -40, -6, -44, -28, -42, 7, 39, 69, 32, 30, -2, 28, 24, 44, 16, 8, 78, 19, 58, -11, 15, 27, 58, -14, 28, 36, 24, 12, 8, 4, 44, 43, 63, 17, 46])
#甘さの好み -100 to 100
coca_y = np.array([-52, -28, -7, 46, -28, -3, -13, 39, -11, 52, 18, 22, -41, 1, -20, 4, 20, 54, -26, 69, -30, 11, -34, 10, -17, -32, 21, -31, 21, -37, -9, -1, -11, 1, -14, -45, 27, 48, -9, 17, 48, 29, 82, -28, 37, 9, -57, 15, -12, -13, 37, -44, 0, 10, -10, -34, -8, 39, -14, -28])
#どちらのコーラが好きか 1:Pコーラ、2:Cコーラ
answer = np.array([1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1, 2, 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2])
# 説明変数の格納 1次元目をcoca_x(炭酸),2次元目をcoca_y(甘さ)とする行列を作成
coca = np.c_[coca_x, coca_y]
print("説明変数を出力\n", coca)
#目的変数の格納
print("目的変数を出力\n", answer)
#学習用データと評価用データに分割
x_train, x_test, y_train, y_test = train_test_split(coca, answer, test_size=0.3,random_state=0)#学習用を7割、評価用を3割に振り分ける
print("学習用の目的変数を出力\n", y_train)
print("学習用の説明変数を出力\n", x_train)
print("評価用の目的変数を出力\n", y_test)
print("評価用の説明変数を出力\n", x_test)
#機械学習モデルに決定木を選択
model = tree.DecisionTreeClassifier()
#機械学習
model.fit(x_train, y_train)
for i in range(len(x_train)):#教師データに分けた後に、散布図を表示させて決定木の結果を検証できるようにする
plt.scatter(x_train[i,0], x_train[i,1], color= 'red' if y_train[i] == 1 else 'blue', marker='o')
#全評価用データを使って予測
predict = model.predict(x_test)
print("評価用全データに対する予測結果を出力\n", predict)
print("評価用全データに対する正解率を出力\n", accuracy_score(y_test, predict))
#推測計算
sample_coca = np.c_[-50, 0]#炭酸の強さが-40, 甘さが-50の人は上記にはいないが、Pコーラの1に分類されるはず
predict = model.predict(sample_coca)
print("炭酸の強さが-50, 甘さが0の人の推測値(1:Pコーラ、2:Cコーラ)\n", predict)
dot_data = StringIO() #dotファイル情報の格納先
export_graphviz(model, out_file=dot_data,
feature_names=["Strength of carbonic acid", "Strength of sweetness"],#炭酸の強さと、酸味の強さ
class_names=["P Cola","C Cola"],#どちらが好きなのか(答え)を表示
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())

#下記は教師用データの散布図(赤がPコーラ、青がCコーラ)
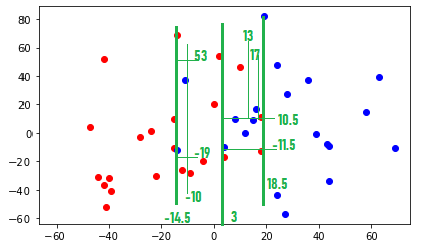
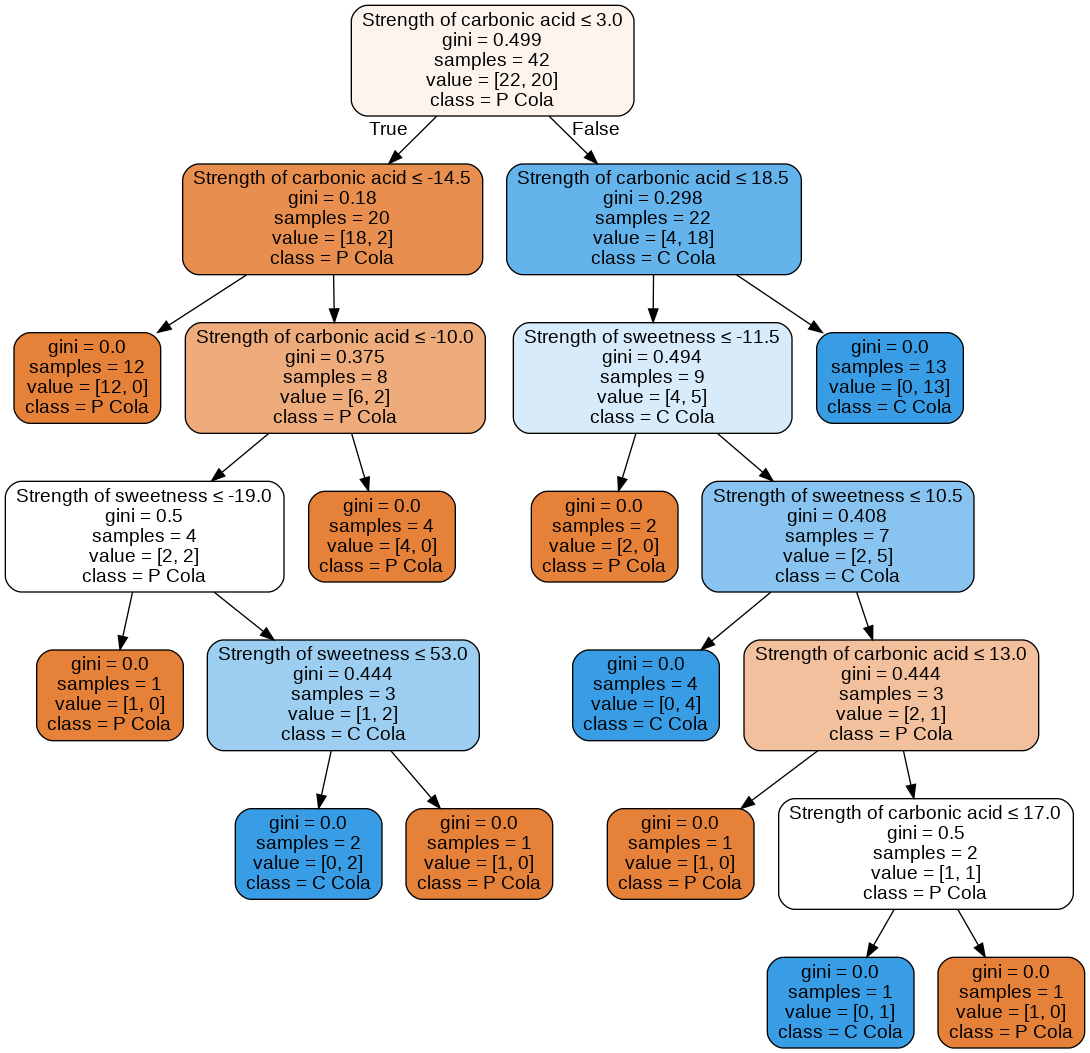
下記は決定木の各ツリー情報(各ツリーの条件によってグループ分けをしている)
まず横軸の炭酸の強さStrength of carbonic acidの値3で、左側にPコーラ、右側にCコーラが好きな人を大きく分けている。value=[22,20]はPコーラが好きな人が22人、Cコーラが好きな人が20人いるという事を示している。その次は横軸-14.5でPコーラが好きな人(12人)を左に分け右側は横軸18.5でCコーラが好きな人(13人)を分けている。このように各データについてグループ分けが行われている。
---------------------------------------
#複数モデル利用が可能な機械学習:教師あり学習
#アンケートを行った結果、Cコーラが好きな人(青)、Pコーラが好きな人(オレンジ)をプロットすると次のようになった。

import numpy as np # 数値計算を効率的に行うためのライブラリ(プログラム群)
import matplotlib.pyplot as plt# データの散布図などグラフ描画を行うライブラリ(プログラム群)
from sklearn.model_selection import train_test_split # 元データを学習用と評価用に自動分割するプログラムを読み込む処理
from sklearn.metrics import accuracy_score # 推測結果を評価をする際に便利なライブラリ(プログラム群)
from sklearn import tree # 決定木を利用する際に必要となるライブラリ(プログラム群)
from sklearn.neural_network import MLPClassifier # ニューラルネットワークNNを利用する際に必要となるライブラリ(プログラム群)
from sklearn import svm # SVMを利用する際に必要となるライブラリ(プログラム群)
from sklearn.linear_model import LogisticRegression # ロジスティクス回帰を利用する際に必要となるライブラリ(プログラム群)
from sklearn.ensemble import RandomForestClassifier # ランダムフォレストを利用する際に必要となるライブラリ(プログラム群)
from sklearn.preprocessing import StandardScaler# データの標準化を行うライブラリ(プログラム群)
#炭酸の強さの好み -100 to 100
coca_x = np.array([ -41, -9, 19, 10, -80, -28, 18, -3, -15, -42, -5, -36, -39, -24, -4, -47, 0, 2, -12, -14, -22, 18, 0, -15, 4, -40, -6, -44, -28, -42, 7, 39, 69, 32, 30, -2, 28, 24, 44, 16, 8, 78, 19, 58, -11, 15, 27, 58, -14, 28, 36, 24, 12, 8, 4, 44, 43, 63, 17, 46])
#甘さの好み -100 to 100
coca_y = np.array([-52, -28, -7, 46, -28, -3, -13, 39, -11, 52, 18, 22, -41, 1, -20, 4, 20, 54, -26, 69, -30, 11, -34, 10, -17, -32, 21, -31, 21, -37, -9, -1, -11, 1, -14, -45, 27, 48, -9, 17, 48, 29, 82, -28, 37, 9, -57, 15, -12, -13, 37, -44, 0, 10, -10, -34, -8, 39, -14, -28])
#どちらのコーラが好きか 1:Pコーラ、2:Cコーラ
answer = np.array([1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1, 2, 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2 , 2])
# 説明変数の格納 1次元目をcoca_x(炭酸),2次元目をcoca_y(甘さ)とする行列を作成
coca = np.c_[coca_x, coca_y]
print("説明変数を出力\n", coca)
#目的変数の格納
print("目的変数を出力\n", answer)
#学習用データと評価用データに分割
x_train, x_test, y_train, y_test = train_test_split(coca, answer, test_size=0.3,random_state=0)#学習用を7割、評価用を3割に振り分ける
print("学習用に振り分けられたデータの目的変数を出力\n", y_train)
print("学習用に振り分けられたデータの説明変数を出力\n", x_train)
print("評価用に振り分けられたデータの目的変数を出力\n", y_test)
print("評価用に振り分けられたデータの説明変数を出力\n", x_test)
#重要な個所:次のコメント操作で分析方法を(決定木、ランダムフォレスト、ニューラル、SVM、ロジスティク回帰)変える。
#model = tree.DecisionTreeClassifier() #機械学習モデルに決定木decision treeを選択:分類木と回帰木を組み合わせたツリー(樹形図)を利用して目的変数を推測する
model = RandomForestClassifier()#機械学習モデルに ランダムフォレストを選択:決定木を大量に利用(平均値等)して目的変数を推測する
#model = MLPClassifier(solver="sgd",random_state=0,max_iter=10000)#機械学習モデルにニューラルネットワークを選択:人間の脳内にある神経細胞(ニューロン)とそのつながりの強弱を模したモデルで目的変数を推測する
#model = svm.SVC()#機械学習にSupport Vector Machine(SVM)を選択:グループ分けをする線に最も近いデータ点を利用して目的変数を推測する
#model = LogisticRegression()#機械学習モデルにLogistic Regressionロジスティック回帰を選択:ロジスティック関数(シグモイド関数)を利用して目的変数(2値に限定)に対して推測を行う
#指定されたモデルで機械学習を実行
model.fit(x_train, y_train)
#-----教師用データの散布図を表示する
for i in range(len(x_train)):#元々のデータを表示する
plt.scatter(x_train[i,0], x_train[i,1], color= 'blue' if y_train[i] == 1 else 'red', marker='o')
plt.xlim([-100, 100]) #x軸の表記メモリ設定
plt.ylim([-100, 100]) #y軸の表記メモリ設定
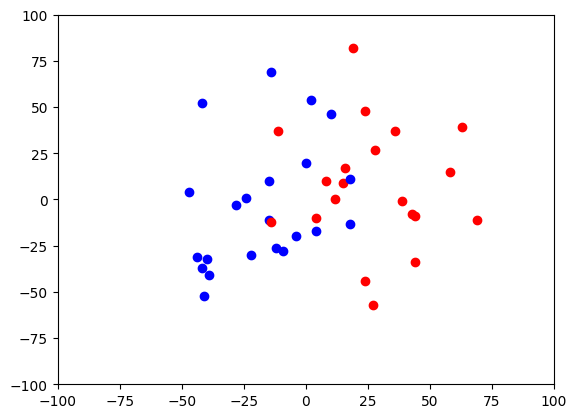
#下の図は教師用データが、コーラ派とペプシ派の散布図 赤がCコーラ、青がPコーラ
print("下の図はAIに教える教師用データの散布図で、赤がCコーラ、青がPコーラ派を示している。(元のデータから乱数を元に70%を教師用データに、30%を評価用データに自動割り振りするので実行する毎に乱数が代わり結果も少し変わります)\n")
plt.show() #グラフ描画
#-----評価用データの散布図を表示する
for i in range(len(x_test)):#元々のデータを表示する
plt.scatter(x_test[i,0], x_test[i,1], color= 'blue' if y_test[i] == 1 else 'red', marker='o')
plt.xlim([-100, 100]) #x軸の表記メモリ設定
plt.ylim([-100, 100]) #y軸の表記メモリ設定
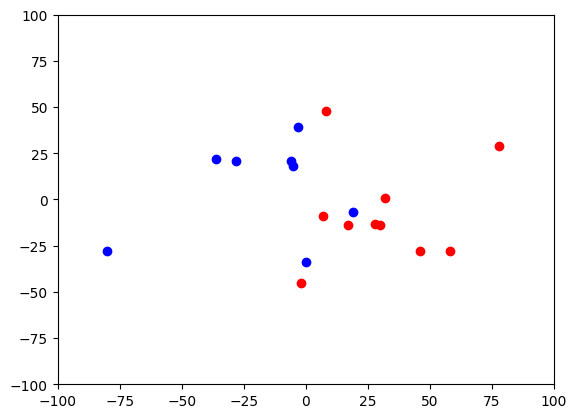
#下の図は評価用データのコーラ派とペプシ派の散布図 赤がCコーラ、青がPコーラ
print("下のAI判定を評価するための評価用データの散布図で、赤がCコーラ、青がPコーラ派を示している。(元のデータから乱数を元に70%を教師用データに、30%を評価用データに自動割り振りするので実行する毎に乱数が代わり結果も少し変わります)\n")
plt.show() #グラフ描画
#-----データの分岐点を表示させる
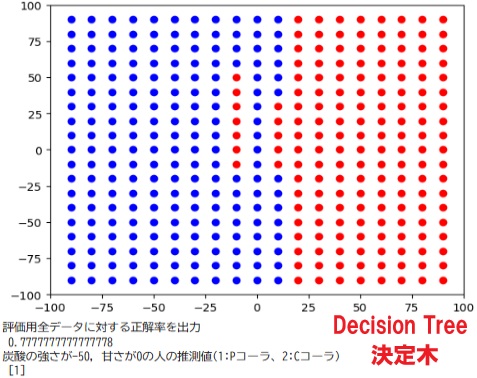
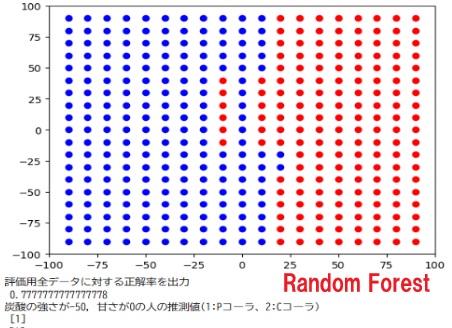
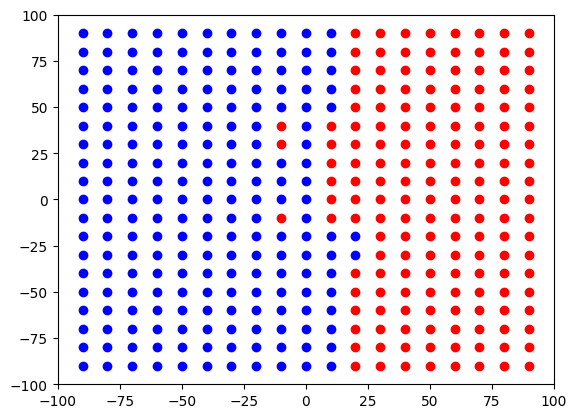
print("下の図は、どこでコーラ派とペプシ派が分かれるかを表示した図 赤がCコーラ、青がPコーラ 直線で分けるモデル、曲線で分けるモデル、曲線ではなく領域で分けるモデル(決定木,ランダムフォレスト)の違いを確認する。\n")
for loop_x in range(-90,100,10):#教師データに分け、xを-90から90まで、10ずつ変化させて、その点のAIの推測結果を表示する(100までとすると、100は実行されない)
for loop_y in range(-90,100,10):#教師データに分け、yを-90から90まで、10ずつ変化させて、その点のAIの推測結果を表示する
sample_coca = np.c_[loop_x, loop_y]
prediction = model.predict(sample_coca)
plt.scatter(loop_x, loop_y, color= 'blue' if prediction == 1 else 'red', marker='o')
plt.xlim([-100, 100]) #x軸の表記メモリ設定
plt.ylim([-100, 100]) #y軸の表記メモリ設定
plt.show() #グラフ描画
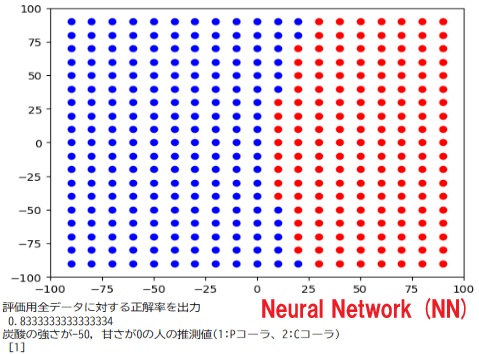
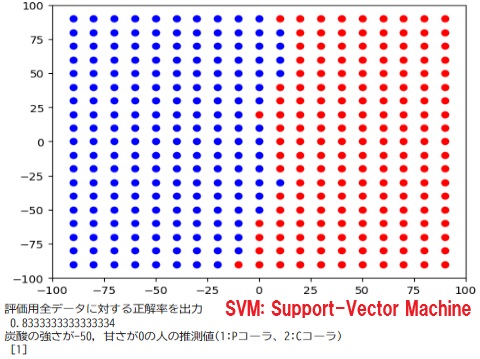
#下の図は、どこでコーラ派とペプシ派が分かれるかを表示した図 赤がCコーラ、青がPコーラ 直線で分けるモデル、曲線で分けるモデル、曲線ではなく領域で分けるモデル(決定木,ランダムフォレスト)の違いを確認する。

#全評価用データを使って予測
print("評価用全データに対する正解率を出力\n", model.score(x_test, y_test))
#推測計算
sample_coca = np.c_[-50, 0]#炭酸の強さが-50, 甘さが0の人は上記にはいないが、Pコーラの1に分類されるはず
predict = model.predict(sample_coca)
print("炭酸の強さが-50, 甘さが0の人の推測値(1:Pコーラ、2:Cコーラ)\n", predict)

#複数モデル利用が可能な機械学習:教師あり学習(データを外部のエクセルファイルから読み込む方法 下記赤色部分が上記プログラムとの変更点)
#次のようにエクセルファイル(右クリックで一度、自分のパソコンにダウンロード)をサーバーにアップロードします。
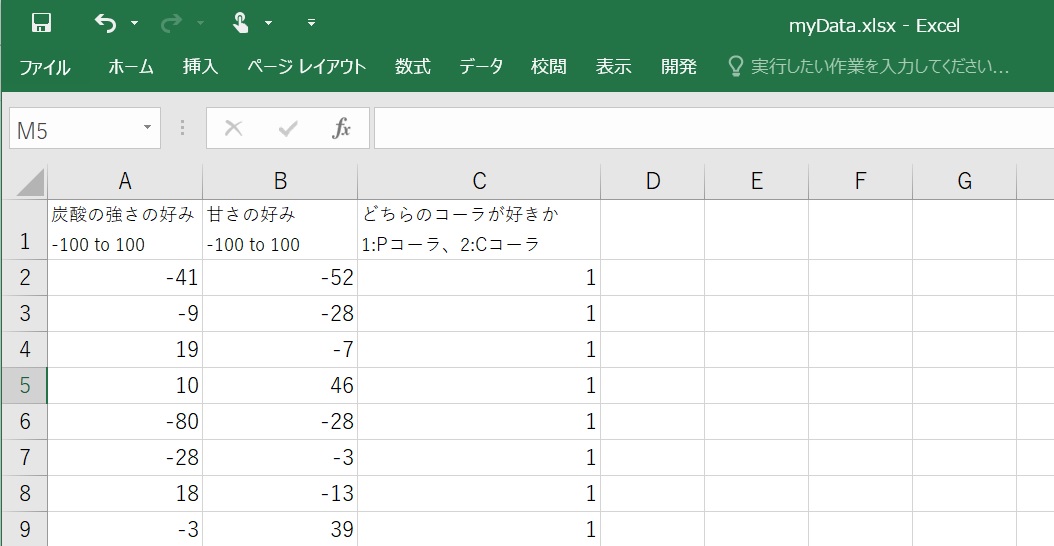
#左のメニューから[フォルダ]をクリックして、[アップロード]アイコンを選択します。
#次に、ファイルを選択して[開く]を押すと、アップロードしたファイルはランタイム・・・というメッセージがでますが、これはデータは一時的に保管されますが、次回接続時は削除されるという事です。ここではOKを押します。次回にこのプログラムを実行する際には、事前に上記と同じ操作をしてデータをアップロードしてから実行して下さい。
#左にmyData.xlsが表示されていますので、プログラムから読み込めるようになりました。
#アンケートを行った結果、Cコーラが好きな人(青)、Pコーラが好きな人(オレンジ)をプロットすると次のようになった。

import numpy as np # 数値計算を効率的に行うためのライブラリ(プログラム群)
import matplotlib.pyplot as plt# データの散布図などグラフ描画を行うライブラリ(プログラム群)
from sklearn.model_selection import train_test_split # 元データを学習用と評価用に自動分割するプログラムを読み込む処理
from sklearn.metrics import accuracy_score # 推測結果を評価をする際に便利なライブラリ(プログラム群)
from sklearn import tree # 決定木を利用する際に必要となるライブラリ(プログラム群)
from sklearn.neural_network import MLPClassifier # ニューラルネットワークNNを利用する際に必要となるライブラリ(プログラム群)
from sklearn import svm # SVMを利用する際に必要となるライブラリ(プログラム群)
from sklearn.linear_model import LogisticRegression # ロジスティクス回帰を利用する際に必要となるライブラリ(プログラム群)
from sklearn.ensemble import RandomForestClassifier # ランダムフォレストを利用する際に必要となるライブラリ(プログラム群)
from sklearn.preprocessing import StandardScaler# データの標準化を行うライブラリ(プログラム群)
import pandas as pd
#df = pd.read_excel('https://toyotani.org/lib/lib/myData.xlsx')#上記のファイルが無くても動くように、インターネット上からエクセルのデータをpandas(pd)というデータ管理ツールを使って読み込みます
df = pd.read_excel('myData.xlsx')#エクセルのデータを読み込む これが本来のプログラムです
#df = pd.read_excel('myData.xlsx','Sheet2', header = None)#エクセルで1番上のデータ項目(見出し/ヘッダ)行が無い場合は、このようにヘッダ無を指定する。Sheet2は読み込むシートを指定してデータを読み込む
np_list = df.to_numpy() #pandasでエクセルファイルを読み込んだ後に、データをnumpyというデータ分析に便利なツールでマトリックスの行列に変換する(アンケートデータを方向に抽出する必要があるため)
#炭酸の強さの好み -100 to 100
coca_x = np_list[:, 0] #1列目(プログラム内では0から始まる)のデータを抽出して coca_xに代入する(炭酸の強さの好み -100 to 100)
#甘さの好み -100 to 100
coca_y = np_list[:, 1] #2列目(プログラム内では1)のデータを抽出して coca_xに代入する(炭酸の強さの好み -100 to 100)
#どちらのコーラが好きか 1:Pコーラ、2:Cコーラ
answer = np_list[:, 2] #3列目(プログラム内では3)のデータを抽出して coca_xに代入する(炭酸の強さの好み -100 to 100)
# 説明変数の格納 1次元目をcoca_x(炭酸),2次元目をcoca_y(甘さ)とする行列を作成
coca = np.c_[coca_x, coca_y]
print("説明変数を出力\n", coca)
#目的変数の格納
print("目的変数を出力\n", answer)
#学習用データと評価用データに分割
x_train, x_test, y_train, y_test = train_test_split(coca, answer, test_size=0.3,random_state=0)#学習用を7割、評価用を3割に振り分ける
print("学習用に振り分けられたデータの目的変数を出力\n", y_train)
print("学習用に振り分けられたデータの説明変数を出力\n", x_train)
print("評価用に振り分けられたデータの目的変数を出力\n", y_test)
print("評価用に振り分けられたデータの説明変数を出力\n", x_test)
#重要な個所:次のコメント操作で分析方法を(決定木、ランダムフォレスト、ニューラル、SVM、ロジスティク回帰)変える。
#model = tree.DecisionTreeClassifier() #機械学習モデルに決定木decision treeを選択:分類木と回帰木を組み合わせたツリー(樹形図)を利用して目的変数を推測する
model = RandomForestClassifier()#機械学習モデルに ランダムフォレストを選択:決定木を大量に利用(平均値等)して目的変数を推測する
#model = MLPClassifier(solver="sgd",random_state=0,max_iter=10000)#機械学習モデルにニューラルネットワークを選択:人間の脳内にある神経細胞(ニューロン)とそのつながりの強弱を模したモデルで目的変数を推測する
#model = svm.SVC()#機械学習にSupport Vector Machine(SVM)を選択:グループ分けをする線に最も近いデータ点を利用して目的変数を推測する
#model = LogisticRegression()#機械学習モデルにLogistic Regressionロジスティック回帰を選択:ロジスティック関数(シグモイド関数)を利用して目的変数(2値に限定)に対して推測を行う
#指定されたモデルで機械学習を実行
model.fit(x_train, y_train)
#-----教師用データの散布図を表示する
for i in range(len(x_train)):#元々のデータを表示する
plt.scatter(x_train[i,0], x_train[i,1], color= 'blue' if y_train[i] == 1 else 'red', marker='o')
plt.xlim([-100, 100]) #x軸の表記メモリ設定
plt.ylim([-100, 100]) #y軸の表記メモリ設定
#下の図は教師用データが、コーラ派とペプシ派の散布図 赤がCコーラ、青がPコーラ
print("下の図はAIに教える教師用データの散布図で、赤がCコーラ、青がPコーラ派を示している。(元のデータから乱数を元に70%を教師用データに、30%を評価用データに自動割り振りするので実行する毎に乱数が代わり結果も少し変わります)\n")
plt.show() #グラフ描画

#-----評価用データの散布図を表示する
for i in range(len(x_test)):#元々のデータを表示する
plt.scatter(x_test[i,0], x_test[i,1], color= 'blue' if y_test[i] == 1 else 'red', marker='o')
plt.xlim([-100, 100]) #x軸の表記メモリ設定
plt.ylim([-100, 100]) #y軸の表記メモリ設定
#下の図は評価用データのコーラ派とペプシ派の散布図 赤がCコーラ、青がPコーラ
print("下のAI判定を評価するための評価用データの散布図で、赤がCコーラ、青がPコーラ派を示している。(元のデータから乱数を元に70%を教師用データに、30%を評価用データに自動割り振りするので実行する毎に乱数が代わり結果も少し変わります)\n")
plt.show() #グラフ描画

#-----データの分岐点を表示させる
print("下の図は、どこでコーラ派とペプシ派が分かれるかを表示した図 赤がCコーラ、青がPコーラ 直線で分けるモデル、曲線で分けるモデル、曲線ではなく領域で分けるモデル(決定木,ランダムフォレスト)の違いを確認する。\n")
for loop_x in range(-90,100,10):#教師データに分け、xを-90から90まで、10ずつ変化させて、その点のAIの推測結果を表示する(100までとすると、100は実行されない)
for loop_y in range(-90,100,10):#教師データに分け、yを-90から90まで、10ずつ変化させて、その点のAIの推測結果を表示する
sample_coca = np.c_[loop_x, loop_y]
prediction = model.predict(sample_coca)
plt.scatter(loop_x, loop_y, color= 'blue' if prediction == 1 else 'red', marker='o')
plt.xlim([-100, 100]) #x軸の表記メモリ設定
plt.ylim([-100, 100]) #y軸の表記メモリ設定
plt.show() #グラフ描画
#下の図は、どこでコーラ派とペプシ派が分かれるかを表示した図 赤がCコーラ、青がPコーラ 直線で分けるモデル、曲線で分けるモデル、曲線ではなく領域で分けるモデル(決定木,ランダムフォレスト)の違いを確認する。
#全評価用データを使って予測
print("評価用全データに対する正解率を出力\n", model.score(x_test, y_test))
#推測計算
sample_coca = np.c_[-50, 0]#炭酸の強さが-50, 甘さが0の人は上記にはいないが、Pコーラの1に分類されるはず
predict = model.predict(sample_coca)
print("炭酸の強さが-50, 甘さが0の人の推測値(1:Pコーラ、2:Cコーラ)\n", predict)

---------------------------------------
#主成分分析(教師無し機械学習)
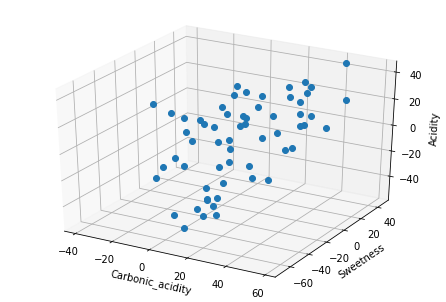
#好きなコーラの味で炭酸の強さ、甘さ、酸味の強さについてアンケートを行った。そのデータを使って主成分分析を行い、主な主成分を算出し、どのような味の好みの人たちが存在するのかを明らかにする。次はアンケート結果を基に、Carbonic_acid(炭酸の強さ) Sweetness(甘みの強さ) Acidity(酸味の強さ)を3次元にプロットした図である(この3次元図ではよく分からない)。
import numpy as np# 数値計算やデータフレーム操作に関するライブラリをインポートする
import pandas as pd
import matplotlib.pyplot as plt #図やグラフを図示するためのライブラリをインポートする
from mpl_toolkits.mplot3d import Axes3D #3次元プロットするためのモジュール
from sklearn.preprocessing import StandardScaler# データ標準化ライブラリ
import sklearn #機械学習の代表的なpythonのライブラリ
from sklearn.decomposition import PCA #主成分分析ツール
from sklearn.cluster import KMeans #クラスタ分類ツール
#入力データ:炭酸の強さ -100 to 100
carbonic_acid = np.array([53, 47, 50, 43, 48, 45, 53, 29, 14, 20, 46, 40, 54, 10, 13, 40, 58, 34, 23, 18, -19, -12, -1, -13, -24, 0, 29, 19, -20, 7, -12, -5, 23, -5, 6, -15, 5, 5, 27, -15, 9, 9, -8, 3, -14, 11, 3, 1, 10, 11, 16, 0, -10, 1, 8, -19, -39, 10, 8, 9])
#入力データ:甘み -100 to 100
sweetness = np.array([-27, -38, -21, 45, -12, -3, -28, 12, -28, -15, 0, 13, 21, -4, 17, 6, -9, -15, -9, -14, -2, 15, 28, -24, -6, 20, 17, 5, 1, 11, -38, -9, 22, 19, -7, 6, -2, -14, 18, 43, -68, -28, -24, -22, -42, 11, -9, -23, 9, -62, -39, -27, 2, -18, -8, 5, 4, -25, 35, -17])
#入力データ:酸味の強さ -100 to 100
acidity = np.array([28, 26, 34, 44, 22, 41, 46, 35, 32, 40, 23, 38, 29, 37, 23, 44, 21, 26, 27, 21, 5, -7, -2, -15, 9, -5, -13, -3, -7, 2, -16, 7, -18, -24, 17, 1, -5, -2, 25, 6, -33, -44, -20, -44, -23, -39, -24, -57, -29, -45, -44, -50, -49, -46, -19, -16, 8, -39, -52, -31])
#入力項目名を設定 Carbonic_acid(炭酸の強さ) Sweetness(甘みの強さ) Acidity(酸味の強さ)
df = pd.DataFrame({'Carbonic_acid': carbonic_acid, 'Sweetness': sweetness, 'Acidity': acidity})
#display(df)#入力データの確認表示
# データを標準化する処理
sc = StandardScaler()
clustering_sc = sc.fit_transform(df)#データを変換するために必要な統計情報を計算して、正規化(標準化)する
std_data_df = pd.DataFrame(clustering_sc, columns = df.columns)#標準化されたデータフレーム(データ)
#display(std_data_df)#データの標準化処理結果を確認する際に表示する
#3次元グラフの枠を描画する
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("Carbonic_acidity")#各軸にラベルを表示
ax.set_ylabel("Sweetness")#各軸にラベルを表示
ax.set_zlabel("Acidity")#各軸にラベルを表示
ax.plot(df.loc[:,'Carbonic_acid'],df.loc[:,'Sweetness'],df.loc[:,'Acidity'],marker="o",linestyle='None')#散布図を描画する際に、linestyle='None'にしないと線が引かれる
plt.show()#最後に.show()を書いてグラフ表示
# KMeansによるクラスタリング分類処理
kmeans = KMeans(n_clusters=3, random_state=0)
clusters = kmeans.fit(clustering_sc)
#print(clusters.labels_)#クラスタリングの分類結果を確認する際に表示する
df['cluster']=clusters.labels_
#sklearnのPCAを利用した主成分分析
pca = PCA()
pca.fit(clustering_sc)
clustering_sc_pca = pca.transform(clustering_sc)
pca_df = pd.DataFrame(clustering_sc_pca)
pca_df['cluster'] = df['cluster']
print(pca_df)#主成分分析PCAの結果を表示
# データを主成分空間に写像
pca_cor = pca.transform(std_data_df)
eig_vec = pd.DataFrame(pca.components_.T, columns=["Principal Component{}".format(x + 1) for x in range(len(std_data_df.columns))] , index = std_data_df.columns)
# 各主成分 因子負荷量 固有ベクトル

display(eig_vec)
#この各主成分の因子負荷量を見ると第1主成分の因子負荷量は炭酸が0.64、酸味が0.7と強めで甘さが0.28と、「炭酸と酸味が強く甘くない」コーラが好きな人達であることがわかる。第2主成分は炭酸がマイナスで甘さが0.91、酸味が0.0と炭酸が弱く甘みが強く、「炭酸が弱く酸味もほどほどで甘みが強い」味のコーラが好きな人達である。第3主成分は炭酸が0.64と強めで甘さが0.29と少し甘いが、酸味が-0.7と「炭酸が強く酸味が全く無く甘くない」コーラが好きな人達であることがわかる。
# 固有値
eig = pd.DataFrame(pca.explained_variance_).T
#display(eig)
# 寄与率
ev = pd.DataFrame(pca.explained_variance_ratio_, index=["Principal Component{}".format(x + 1) for x in range(len(std_data_df.columns))], columns=['寄与率']).T

display(ev)
# 累積寄与率
t_ev = pd.DataFrame(pca.explained_variance_ratio_.cumsum(), index=["Principal Component{}".format(x + 1) for x in range(len(std_data_df.columns))], columns=['累積寄与率']).T

display(t_ev)
#第1主成分から第3主成分までの累計が1になっているため、元のデータは第1主成分から第2、第3主成分で構成されている事が分かる。
# 主成分得点
print('主成分得点')
cor = pd.DataFrame(pca_cor, columns=["Principal Component{}".format(x + 1) for x in range(len(std_data_df.columns))])
display(cor)
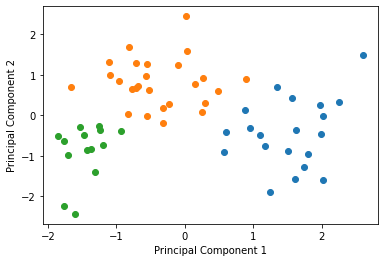
for i in df['cluster'].unique():#第一主成分と第二主成分でプロットする
tmp = pca_df.loc[pca_df['cluster'] == i]
plt.scatter(tmp[0], tmp[1])
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.show()
# 累積寄与率を図にして表示する
import matplotlib.ticker as ticker
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("Number of Principal Component")
plt.ylabel("Cumulative contribution rate")
plt.grid()
plt.show()
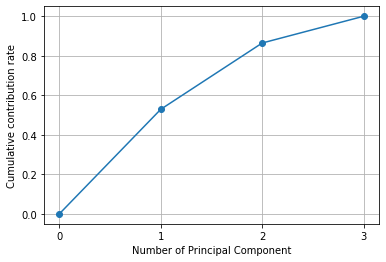
#上記の表と同じであるが、それを図示すると上のようになり、第1主成分から第3主成分までの累計寄与率が1になっているため、元のデータは第1主成分が53%を占め、第2が34%、第3主成分までを合わせると100%に達する事が分かる。
その他
数値シミュレーションエクセルファイル
数値シミュレーションJavaファイル
数値シミュレーション2次元解析Javaファイル
|












































